Bitwise nuggets: rotate a number to the left using bit precision

Here we discuss how to rotate a number to the left by k positions, using bit precision. (In a previous post we’ve seen the same problem, but the rotation involved byte precision.)

What does that even mean? We want to left-shift the number by k bits, but the most significant k bits that overflow as a result of the left-shift operation must be saved and added to the k least significant bits of the left-shifted number (these bits are zero after the left-shift). In addition, the rotation has bit precision, meaning we left-shift on the precise number of bits that the number requires for its representation.

Let us see an example to better visualize the rotation to the left. Suppose we want to rotate the number 100 to the left by 3 positions. As shown below, when using bit precision, we expect to obtain 38:

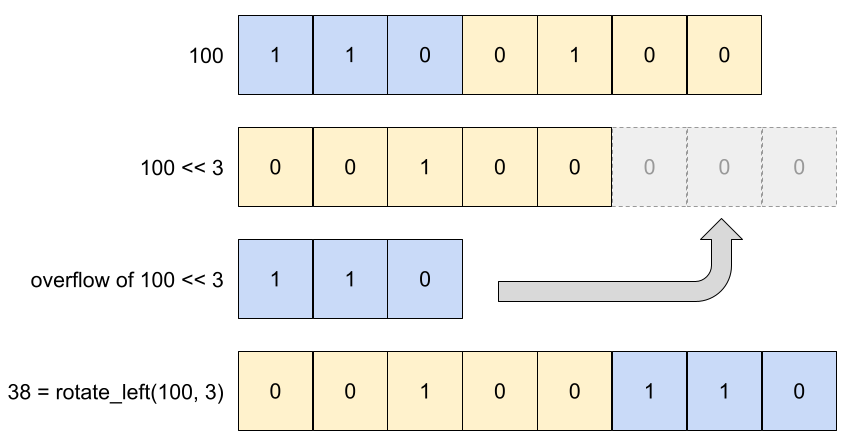
Since we’re using bit precision, the actual overflow when 100 is left-shifted by 3 positions is 110 (i.e. decimal 6).

Here are the steps for solving this problem:

1. determine the number of bits that the number requires
2. compute the overflow, or the k MSB of the number
3. left-shift the number by k positions
4. add the overflow to the left-shifted number

First, we need a helper function to count the number of bits needed to represent a given number. Here is the idea: while the number is non-zero, we divided it by two (in other words, we right-shift it by 1 position) and increment the number of bits that we’ve counted so far.

1
2
3
4
5
6
7
8
9
10

// Determine the number of bits that the given `number` requires.
unsigned int count_total_bits(unsigned int number)
{
    unsigned int bits = 0;
    while (number) {
        number >>= 1;
        ++bits;
    }
    return bits;
}

We can now implement rotation to the left using bit precision:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

// Rotate the given `number` to the left by `k` positions. Rotation takes place on
// the precise number of bits needed to represent the `number`.
unsigned int rotate_left_bit_precision(unsigned int number, unsigned int k)
{
    // Determine the number of bits needed to represent the `number`.
    unsigned int precision = count_total_bits(number);

    // Overflowing bits are the most significant ones. Right-shift by precision - k bits.
    unsigned int overflow = number >> (precision - k);

    // Left-shift `number` by `k` bits.
    unsigned int left_shifted = number << k;

    // Clear the unneeded bytes.
    if (precision < CHAR_BIT * sizeof(unsigned int))
        left_shifted &= (unsigned int) ((1 << precision) - 1);

    // Add the overflow.
    return left_shifted | overflow;
}

At lines 6 we determine the precision, i.e. the number of bits required to represent the number. We use the precision for determining the overflow bits at line 9. Then we shift the number by k positions to the left at line 12. At lines 15-16, we ensure that the MSB are zeroed out if the number is represented on less than 32 bits. Finally, at line 19 we add the overflow to the left_shifted number using the logical OR operator.

Here are some examples of left rotation on bit precision in action:

1
2
3
4
5
6

rotate_left_bit_precision(       100,  3) =         38
rotate_left_bit_precision(       244,  3) =        167
rotate_left_bit_precision(       356, 10) =          0
rotate_left_bit_precision(      2019,  4) =       1599
rotate_left_bit_precision(    983396,  8) =      91376
rotate_left_bit_precision(3422643215,  5) = 2150400505

Want to see more bitwise logic? There’s a whole repository on my GitHub on bit fiddling.