Bitwise nuggets: insert a number inside another one

Here we discuss how to insert a number m into a number n between positions i and j.

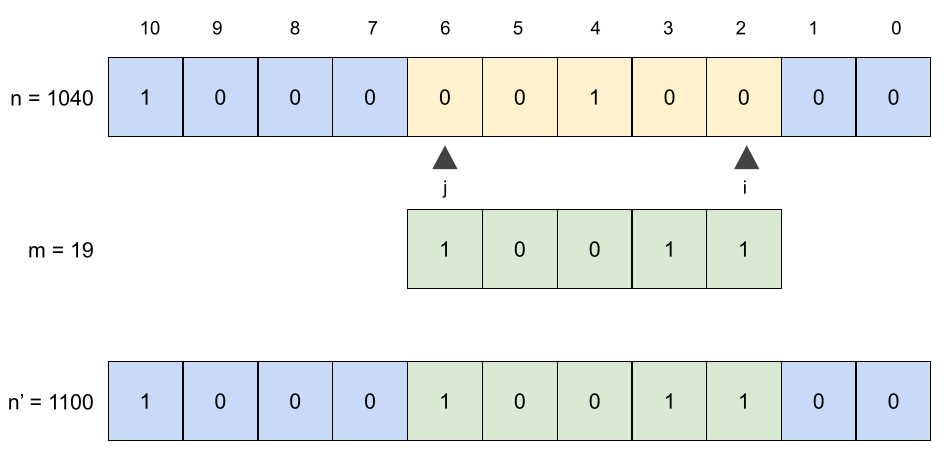
Let us see an example to better visualize what this means. Suppose we have the number n = 1040 and that we want to insert the number m = 19 into it, between positions i = 2 and j = 6. As shown below, by doing so we obtain the number 1100:

We could go about this in a number of different ways. We’ll just do lazy here , meaning we make two very generous assumptions:

1. The number of bits between i and j is indeed the actual number of bits in number m.
2. There are enough bits in n for inserting m into it.

With that out of the way, we can now focus on the task at hand. The tricky part is to zero-out the bits in number n between positions i and j (in yellow in the figure above). To do this, we must create a bit mask that goes from 0 through j and that has two parts:

• The “left”-most part (between positions i and j) is all zeros (we want to zero-out this part of n). We can obtain it by left-shifting 1 by j + 1 bits, subtracting 1, and finally inverting (logical NOT) the mask.
• The “right”-most part (between positions 0 and i - 1) is all ones (we want to keep this part of n). We can obtain it by left-shifting 1 by i bits, then subtracting 1.

Once that’s done, we must bring together the two parts of the mask using the logical OR operator.

Next, we apply the mask to the number n, thus clearing its bits at positions i through j. Now the only thing that’s left is to “insert” m into n between these indexes, which we can do by left-shifting m by i bits, followed by applying the logical OR operator.

Here is how this algorithm can be implemented in C:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

// Insert number `m` into number `n` between positions `j` through `i`.
// Assumption 1: the number of bits between `j` and `i` is the number of bits of `m`.
// Assumption 2: there are enough bits in `n` for inserting `m`.
int insert_number_inside_another(int n, int m, int i, int j)
{
    /*
    Create a mask that zeroes out bits from positions j through i (inclusive)
    in n when using the AND operator between n and the mask.
    The mask has the following form:
          Mask:        1   ...  1   0   ...   0   1   ...   1
          Positions: |n|-1     j+1  j         i  i-1        0
    */
    int mask = ~((1 << (j + 1)) - 1) | ((1 << i) - 1);

    // Apply the mask to turn off bits betwene j and i, then insert m.
    return (n & mask) | (m << i);
}

Whew, that long explanation for only 2 lines of actual code, who would have thought?

Want to see more bitwise logic? There’s a whole repository on my GitHub on bit fiddling.