Bitwise nuggets: check if a number is a power of 2

Here we discuss how to determine whether a given number is a power of 2.

As we know, a number is a power of 2 if it has only one of its bits set to 1. Such numbers have a very interesting property that we use all the time for creating bit masks: if we subtract 1 from a power of 2, we get a sequence of 1s starting from the next most significant bit with respect to the bit that is set in out input number.

If we apply the logical AND operator to the input number and this sequence of 1s, we get 0. For a number that is not a power of 2, applying the AND operator to the number and the number from which we subtract 1 will always result in a value different from zero.

Let us see a couple of examples to better visualize what this means.

Here, we can see that 64 is a power of 2 since the bitwise AND with 63 yields all zeros:

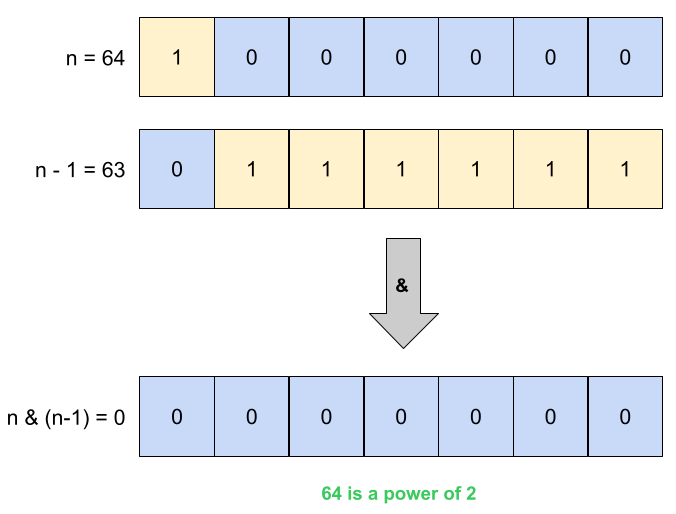
When a number is not a power of 2, the bitwise AND between that number and the number from which we subtract 1 will always yield something other than zero:

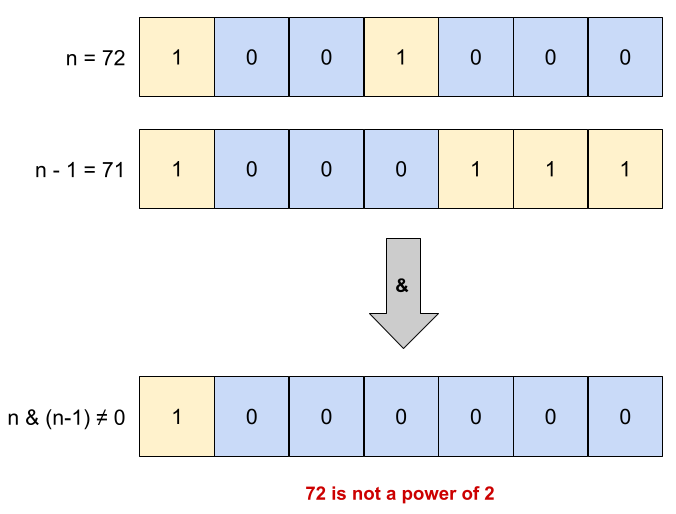
Here is how this algorithm can be implemented in C:

1
2
3
4
5
6
7

#include <stdbool.h>
// Determines whether the specified number is a power of two.
bool is_power_of_two(int number)
{
    if (number == 0) return false;
    return (number & (number - 1)) == 0;
}

Want to see more bitwise logic? There’s a whole repository on my GitHub on bit fiddling.