Bitwise nuggets: flip bit to win

Given an integer, suppose we can flip exactly one of its bits from 0 to 1. We need to determine the longest sequence of 1s that can be obtained.

Let us first see some examples:

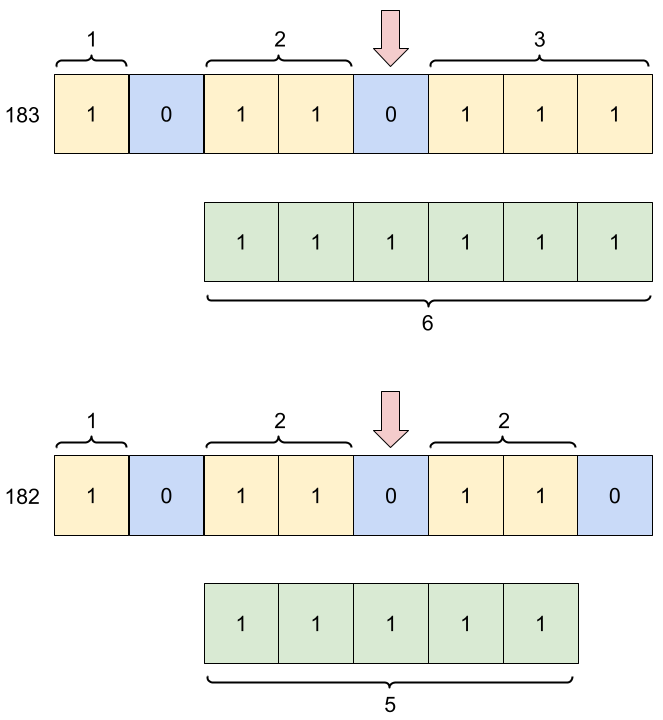
• For number 183 (10110111), the answer is 6. Explanation: there are two 0 bits; going from MSB to LSB:
  • If we flip the first 0 bit to 1, we get a sequence of 1s of length 4.
  • If we flip the second 0 bit to 1, we get a sequence of 1s of length 6.
• For number 182 (10110110), the answer is 5. Explanation: there are three 0 bits; going from MSB to LSB:
  • If we flip the first 0 bit to 1, we get a sequence of 1s of length 4.
  • If we flip the second 0 bit to 1, we get a sequence of 1s of length 5.
  • If we flip the third 0 bit to 1, we get a sequence of 1s of length 3.

How do we solve this problem? The idea is to first count the runs of 0s and 1s in the input number. Since the number is an integer, we assume that its MSB bits up to the 32nd one are all 0s. We then traverse these sequences and decide which is the longest one that we can obtain if we only flip one bit from 0 to 1.

For example, for number 183, we start from the LSB and we count:

• a sequence of 1s of length 3;
• a sequence of 0s of length 1;
• a sequence of 1s of length 2;
• a sequence of 0s of length 1;
• a sequence of 1s of length 1;
• a sequence of 0s of length 24.

Examining this sequence, we decide that since we have a sequence of 1s of length 3 and a sequence of 1s of length 2 separated by a single 0 bit, the longest sequence of 1s that we can obtain by flipping a single bit is 3 + 1 + 2 = 6.

Here is how we can implement this is C:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

// Returns the longest sequence of 1s that can be obtained from `number`
// by flipping one of its bits from 0 to 1.
int flip_bit_to_win(int number)
{
    int seq_lengths[32][2];           // will store lengths of sequences of 0s and 1s
    int seq_counter = 0;              // number of sequences in `seq_lengths` + 1
    int current_value = number & 1;   // current bit value (0 or 1)

    for (size_t i = 0; i < 32; i++)   // all sequence lengths are initially 0
        seq_lengths[i][0] = seq_lengths[i][1] = 0;
    seq_lengths[0][0] = current_value;

    for (size_t i = 0; i < 32; i++) {
        if ((number & 1) == current_value) {  // still in the same sequence as before
           seq_lengths[seq_counter][1]++;
        } else {                              // reading a different sequence now
            seq_lengths[++seq_counter][1] = 1;
            current_value = number & 1;
            seq_lengths[seq_counter][0] = current_value;
        }
        number >>= 1;                         // move on to the next bit
    }

    ++seq_counter;                            // add the MSBs that are 0

    // Determine the longest sequence of 1s that can be obtained by flipping 1 bit
    int max_len = 0;

    for (int i = 0; i < seq_counter; ++i) {
        int curr_max = seq_lengths[i][0] == 0 ? 1 : seq_lengths[i][1];
        if (i < seq_counter - 1)
            curr_max += seq_lengths[i][0] == 1 ? 1 : seq_lengths[i+1][1];
        if (seq_lengths[i][0] == 1 && seq_lengths[i+1][1] == 1 && i < seq_counter - 2)
            curr_max += seq_lengths[i+2][1];
        if (max_len < curr_max)
            max_len = curr_max;
    }

    return max_len;
}

Here are the variables that we use:

• At line 5, we declare seq_lengths, a 2D array where values in the first column are either 0 or 1 (the type of sequence), and values in the second column are the counts of 0s or 1s.
• At line 6, seq_counter represents the number of sequences in seq_lengths.
• At line 7, current_value represents the type of the current sequence: 0 or 1, depending on the value of the LSB in the input number.

At lines 9-11 we initialize the seq_lengths array. We must remember to set the type of the first sequence (line 11) to the current value of the LSB.

We traverse the input number once from its LSB to its MSB and fill in the seq_lengths array (lines 13-22). At each step, we determine the least significant bit (either 0 or 1) and we compare it to the current value. If it is the same as before (lines 14-15), we increment the count of that particular sequence. If it is a different value than before, it means we’re done reading the previous sequence so we update the seq_counter and the curr_value (lines 16-20). We “traverse” the input number bit by bit by right-shifting it at each step (line 21).

In order to properly account for the MSBs that are 0, we need to increment seq_counter once we’re done traversing the input number (line 24).

We now have the runs of 0s and 1s properly stored in the seq_lengths array. At lines 27-39, we determine the longest sequence of 1s that can be obtained by flipping one bit from 0 to 1. We traverse seq_lengths and we determine the current maximum length at each step:

• Line 30: the current maximum is 1 if we’re in a sequence of 0s, or the count of 1s if we’re in a sequence of 1s.
• Lines 31-32: if we’re not handling the last sequence, then we add 1 to the current maximum if we’re in a sequence of 1s (since we know at least a 0 follows) or the number of 1s in the next sequence if we’re in a sequence of 0s (since we know the next sequence has only 1s).
• Lines 33-34: if we’re in a sequence of ones followed by a single 0 bit and there are at least 2 more sequences, then the we add the number of 1s in the next sequence of 1s to the current maximum.
• Lines 35-36: we update the maximum sequence length according to the value of the current maximum.

Here are some test cases:

1
2
3
4
5
6
7
8
9
10
11
12

flip_bit_to_win(  183) =>  6
flip_bit_to_win(  182) =>  5
flip_bit_to_win(  615) =>  4
flip_bit_to_win( 9967) =>  8
flip_bit_to_win(52975) =>  8
flip_bit_to_win(    0) =>  1
flip_bit_to_win(    1) =>  2
flip_bit_to_win(    2) =>  2
flip_bit_to_win(   30) =>  5
flip_bit_to_win(   31) =>  6
flip_bit_to_win(   -1) => 32
flip_bit_to_win(   -2) => 32

Want to see more bitwise logic? There’s a whole repository on my GitHub on bit fiddling.